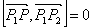Косое произведение векторов
Псевдоскалярным или косым произведением векторов на плоскости называется число $$[a, b] = |a||b|sin(theta)$$
Где $$theta$$ -угол вращения (против часовой стрелки) от a к b. Если хотя бы один из векторов a и b нулевой, то полагают [a, b] = 0.
Если векторы заданы своими координатами a(x1, y1), b(x2, y2) то косое произведение [a, b] = x1y2 — x2y1.
Геометрически косое произведение векторов представляет собой ориентированную площадь параллелограмма, натянутого на эти вектора.
Задача 1
В этой задаче нужно просто проверить неравенство треугольника. А именно: a + b > c, a + c > b, b + c > a.
Задача 2
Первое очевидное решение - вычислить длины сторон и свести эту задачу к Задаче 1. Но при вычислении длин нам нужно использовать операцию взятия корня, а это может привести к неточностям, которые могут повлиять на ответ. Поэтому мы будем решать задачу иначе.
По координатам точек вычислим координаты векторов. Далее вычислим попарно косое произведение найденных векторов. Если ни одно из них не равно нулю, значит треугольник существует.
double vx1 = x1 - x2;
double vy1 = y1 - y2;
double vx2 = x2 - x3;
double vy2 = y2 - y3;
double vx3 = x3 - x1;
double vy3 = y3 - y1;
if (vx1 * vy2 - vx2 * vy1 == 0)
{
Console.WriteLine("NO");
} else
if (vx2 * vy3 - vx3 * vy2 == 0)
{
Console.WriteLine("NO");
} else
if (vx3 * vy1 - vx1 * vy3 == 0)
{
Console.WriteLine("NO");
} else
{
Console.WriteLine("YES");
}
Задача 3
Напротив большей стороны лежит больший угол - это известный факт. Если мы узнаем, чему равен этот больший угол, то сможем понять, какого типа наш треугольник.
Вспомним теорему косинусов:
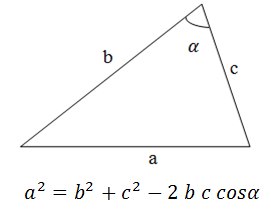
Для решения этой задачи нам не нужно искать значение косинуса, нужно лишь найти его знак. Очевидно, что если косинус угла больше нуля то угол меньше 90°, если он равен нулю, то угол равен 90°, если он меньше нуля, то угол больше 90°.
- Если $$cosa > 0$$, то $$a^2<b^2+c^2$$ - треугольник острый
- Если $$cosa = 0$$, то $$a^2=b^2+c^2$$ - треугольник прямоугольный
- Если $$cosa < 0$$, то $$a^2>b^2+c^2$$ - треугольник тупоугольный
Задача 4
Эта задача полностью сводится к предыдущей. Но решение можно упростить. Вид угла легко определяется по знаку скалярного произведения образующих его векторов: оно положительно для острого угла, равно нулю для прямого угла и отрицательно для тупого угла. Поэтому необходимо посчитать все три скалярных произведения, перемножить их и по знаку данного числа определить тип треугольника.
Пусть наш треугольник состоит из трёх векторов, которые мы пронумеруем. Тогда:
//1 и 3
double vx1 = x2 - x1;
double vy1 = y2 - y1;
double vx2 = x3 - x1;
double vy2 = y3 - y1;
double skal1 = vx1 * vx2 + vy1 * vy2;
//2 и 1
vx1 = x1 - x2;
vy1 = y1 - y2;
vx2 = x3 - x2;
vy2 = y3 - y2;
double skal2 = vx1 * vx2 + vy1 * vy2;
//2 и 3
vx1 = x1 - x3;
vy1 = y1 - y3;
vx2 = x2 - x3;
vy2 = y2 - y3;
double skal3 = vx1 * vx2 + vy1 * vy2;
double skalVse = skal1 * skal2 * skal3;
if (skalVse > 0)
{
Console.WriteLine("Острый");
} else if (skalVse == 0)
{
Console.WriteLine("Прямой");
} else
{
Console.WriteLine("Тупой");
}
Задача 5
Решение задачи заключается в применении формулы Герона.
Задача 6
Вспомним о том, что косое произведение двух векторов определяет ориентированную площадь параллелограмма, натянутого на эти вектора. Поскольку диагональ параллелограмма разбивает его на два равновеликих треугольника, то можем найти площадь нашего треугольника, как половину площади параллелограмма.
Задача 7
Метод площадей
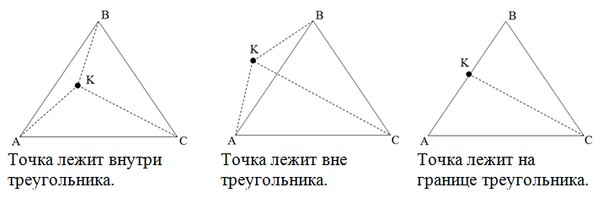
Если сумма площадей треугольников AKB, AKC, BKC (не ориентированных, а «обычных») больше площади треугольника ABC точка лежит вне треугольника. Если же сумма первых трех площадей равна четвертой, то нужно проверить, не равна ли нулю одна из трех площадей. Если равна, то точка лежит на границе треугольника, иначе – внутри.
Вычислять площади треугольников, естественно, надо через косое произведение векторов. Этот метод не очень хороший. Поскольку здесь используются сравнение чисел с плавающей точкой, а это в свою очередь может привести к принятию неверного решения при сравнении. Второй метод опять таки опирается на вектора, он намного эффективнее во всех отношениях.
Проверка полуплоскостей
Если хотя бы одна из сторон треугольника «разводит» противолежащую ей вершину и точку по разным полуплоскостям, то точка лежит вне треугольника. Иначе, если точка принадлежит хотя бы одной из прямых, содержащих стороны треугольника, то она находится на границе треугольника. Иначе точка лежит внутри треугольника.
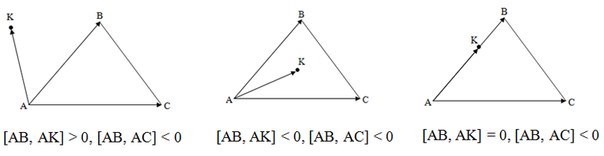
В первом примере сторона AB разводит вершину C и точку K по разным полуплоскостям, поэтому точка лежит снаружи.
Задача 8
Под многоугольником будем подразумевать простой многоугольник, то есть без самопересечений. При этом он может быть как выпуклым, так и не выпуклым.
Данную задачу можно решить двумя способами: вычисляя ориентированные площади трапеций (метод трапеций) и треугольников (метод треугольников).
Метод трапеций
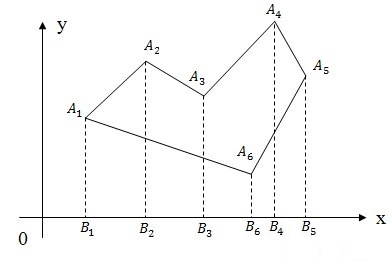
Метод трапеций заключается в разбиении многоугольника на трапеции (как показано на рисунке) и нахождении суммы ориентированных площадей полученных трапеций. Площадь трапеции считается как полусумма оснований на высоту.
for (int i = 1; i <= dots.Length; i++)
{
double Si;
if (i == dots.Length)
{
Si = (dots[0].y + dots[i - 1].y) / 2 * (dots[0].x - dots[i - 1].x);
}
else
{
Si = (dots[i].y + dots[i - 1].y) / 2 * (dots[i].x - dots[i - 1].x);
}
S += Si;
}
Console.WriteLine(Math.Abs(S));
Поскольку полученная площадь является ориентированной, необходимо вычислить ее модуль.
Метод треугольников
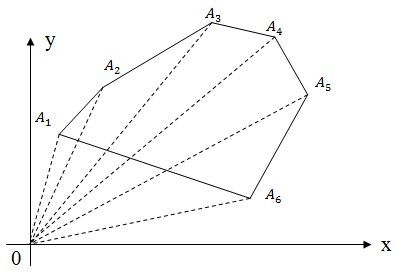
При использовании этого метода мы разбиваем наш многоугольник на треугольники, ищем сумму ориентированных площадей треугольников. Ответом будет модуль этой суммы. Площади треугольников мы ищем с помощью косого произведения векторов.
Задача 9
Многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону.

Задача опять сводится к вычислению косого произведения векторов, а именно у выпуклого многоугольника знаки косых произведений$$$$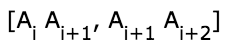 либо положительны, либо отрицательны. Поэтому если мы знаем направление обхода, то знак косых произведений для выпуклого многоугольника одинаков: он неотрицателен при обходе против часовой стрелки и неположителен при обходе по часовой стрелки.
либо положительны, либо отрицательны. Поэтому если мы знаем направление обхода, то знак косых произведений для выпуклого многоугольника одинаков: он неотрицателен при обходе против часовой стрелки и неположителен при обходе по часовой стрелки.
Задача 10
Сама формула: $$S = L + B / 2 - 1$$, где $$L$$ - число целочисленных точек внутри многоугольника, $$B$$ - количество целочисленных точек на его границе, $$S$$ - искомая площадь.
Вывод формулы (http://hijos.ru/2011/09/14/formula-pika/
Сначала заметим, что формула Пика верна для единичного квадрата. Действительно, в этом случае мы имеем $$L=0, B=4$$ и $$S=0+4/2-1=1$$.
Рассмотрим прямоугольник со сторонами, лежащими на линиях решетки. Пусть длины его сторон равны  и
и  . Имеем в этом случае
. Имеем в этом случае  и, по формуле Пика,
и, по формуле Пика,
Рассмотрим теперь прямоугольный треугольник с катетами, лежащими на осях координат. Такой треугольник получается из прямоугольника со сторонами и
и , рассмотренного в предыдущем случае, разрезанием его по диагонали. Пусть на диагонали лежат
, рассмотренного в предыдущем случае, разрезанием его по диагонали. Пусть на диагонали лежат целочисленных точек. Тогда для этого случая
целочисленных точек. Тогда для этого случая и получаем, что
и получаем, что
Теперь рассмотрим произвольный треугольник. Его можно получить, отрезав от прямоугольника несколько прямоугольных треугольников и, возможно, прямоугольник. Поскольку и для прямоугольника, и для прямоугольного треугольника формула Пика верна, мы получаем, что она будет справедлива и для произвольного треугольника.
Остается сделать последний шаг: перейти от треугольников к многоугольникам. Любой многоугольник можно разбить на треугольники (например, диагоналями). Поэтому нужно просто доказать, что при добавлении любого треугольника к произвольному многоугольнику формула Пика остается верной.
Пусть многоугольник и треугольник
и треугольник имеют общую сторону. Предположим, что для
имеют общую сторону. Предположим, что для формула Пика справедлива, докажем, что она будет верна и для многоугольника, полученного из
формула Пика справедлива, докажем, что она будет верна и для многоугольника, полученного из добавлением
добавлением . Так как
. Так как и
и имеют общую сторону, то все целочисленные точки, лежащие на этой стороне, кроме двух вершин, становятся внутренними точками нового многоугольника. Вершины же будут граничными точками. Обозначим число общих точек через
имеют общую сторону, то все целочисленные точки, лежащие на этой стороне, кроме двух вершин, становятся внутренними точками нового многоугольника. Вершины же будут граничными точками. Обозначим число общих точек через и получим
и получим
 — число внутренних целочисленных точек нового многоугольника,
— число внутренних целочисленных точек нового многоугольника,
 — число граничных точек нового многоугольника.
— число граничных точек нового многоугольника.
Из этих равенств получаем

Так как мы предположили, что теорема верна для и для
и для по отдельности, то
по отдельности, то




Тем самым, формула Пика доказана.
Задача 11
Понятно, что если прямая задана своим уравнением ax + by + c = 0, то тут и решать нечего. Достаточно подставить координаты точки в уравнение прямой и проверить чему оно равно. Если больше нуля, то точка находится в верхней полуплоскости, если равна нулю, то точка находится на прямой и если меньше нуля, то точка находится в нижней полуплоскости. Интереснее случай, когда прямая задана, задана координатами двух точек назовем их 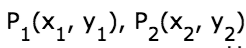
В этом случае можно спокойно найти коэффициенты a, b и c и применить предыдущее рассуждение. Но надо сначала подумать, оно нам надо? Конечно, нет! Как я говорил косое произведения — это просто жемчужина вычислительной геометрии. Давайте применим его. Известно, что косое произведение двух векторов положительно, если поворот от первого вектора ко второму идет против часовой стрелки, равно нулю, если векторы коллинеарны и отрицательно, если поворот идет по часовой стрелки. Поэтому нам достаточно посчитать косое произведение векторов
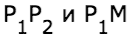
и по его знаку сделать вывод.

Задача 12
Для начала, луч - это прямая, ограниченная точкой с одной стороны и бесконечная с другой. То есть луч задается некоторой начальной точкой и любой точкой лежащей на нем. Очевидно, что если точка принадлежит лучу, то она принадлежит и прямой, проходящей через эти точки, но не наоборот.
Чтобы проверить, принадлежит ли какая-либо точка лучу, нужно проверить косое и скалярное произведения.

Чтобы точка M лежала на луче с начальной точкой P1, где точка P2 лежит на луче, необходимо и достаточно выполнение двух условий:
- $$[P1P2;P1M] = 0$$ - косое произведение (точка лежит на луче)
- $$(P1P2,P1M) \ge 0$$ - скалярное произведение (точка лежит на луче)
Задача 13
Пусть точки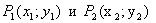 - начальная и конечные точки отрезка.
- начальная и конечные точки отрезка.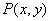 - произвольная точка на плоскости.
- произвольная точка на плоскости.
Вектор с началом в точке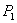 и концом в точке
и концом в точке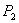 будет иметь координаты (x2-x1, y2-y1).
будет иметь координаты (x2-x1, y2-y1).
Если P(x, y) – произвольная точка, то координаты вектора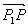 равны: (x-x1, y – y1).
равны: (x-x1, y – y1).
Точка Р будет принадлежать отрезку если:
Векторы в
![clip\_image010\[1\]](http://gospodaretsva.com/wp-content/uploads/2012/03/clip_image0101_thumb.gif)
и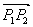
коллинеарны (равно нулю их векторное произведение):Абсцисса точки P удовлетворяет условию:
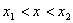
или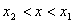
Иначе точка будет находиться на прямой левее или правее отрезка.
Задача 14
Эта задача решается очень легко. Возьмём любую точку на нашей прямой и найдем координаты двух векторов с началом в этой точке и концами в точках, взаимное расположение которых нужно узнать. Далее находим косые произведения вектора, лежащего на данной прямой, с полученными векторами. Находим произведение найденных косых произведений.
- $$[P1P2,P1M1]*[P1P2,P1M2]<0$$ - точки лежат по разные стороны
- $$[P1P2,P1M1]*[P1P2,P1M2]>0$$ - точки лежат по одну сторону
- $$[P1P2,P1M1]*[P1P2,P1M2]=0$$ - одна или две точки лежат на прямой
Задача 15

Задача 16
Отрезки пересекаются тогда, когда, концы каждого отрезка лежат по разные стороны от другого отрезка, либо один из концов одного отрезка лежит на другом.
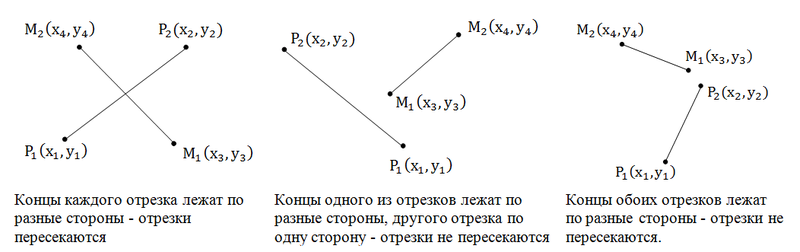 Следовательно нам нужно проверить, чтобы концы каждого отрезка лежали по разные стороны относительно другого отрезка. Это делается при помощи косого произведения. $$[P1P2,P1M1][P1P2,P1M2]<0$$ и аналогично $$[M1M2,M1P1][M1M2,M1P2]<0$$. Важно, что знак в неравенствах строгий. Потому что возможен случай, когда достигается равенство нулю, но отрезки при этом не пересекаются:
Следовательно нам нужно проверить, чтобы концы каждого отрезка лежали по разные стороны относительно другого отрезка. Это делается при помощи косого произведения. $$[P1P2,P1M1][P1P2,P1M2]<0$$ и аналогично $$[M1M2,M1P1][M1M2,M1P2]<0$$. Важно, что знак в неравенствах строгий. Потому что возможен случай, когда достигается равенство нулю, но отрезки при этом не пересекаются:
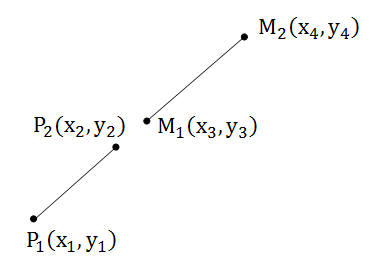
Поэтому нам необходимо сделать еще одну проверку, а именно: принадлежит ли хотя бы один конец каждого отрезка другому (принадлежность точки отрезку). Эту задачу мы уже решали.
Итак, для того чтобы отрезки имели общие точки необходимо и достаточно:
Концы отрезков лежат по разные стороны относительно другого отрезка.
Хотя бы один из концов одного отрезка принадлежит другому отрезку.
Задача 17

Задача 18
Основная загвоздка этой задачи состоит в том, что перпендикуляр не всегда падает на луч, и тогда необходимо найти расстояние от данной точки до начала луча.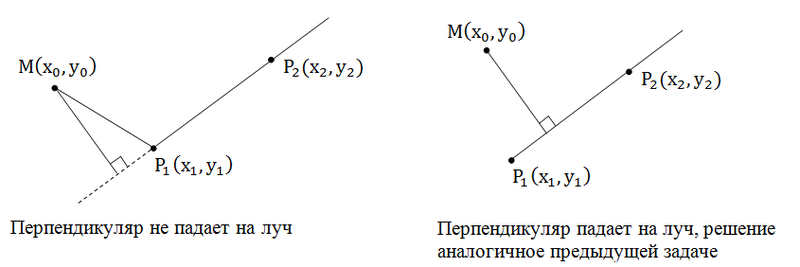 Как же определить падает ли перпендикуляр на луч или нет? Если перпендикуляр не падает на луч, то угол $$MP1P2$$ – тупой иначе острый или прямой. Поэтому по знаку скалярного произведения векторов мы можем определить попадает ли перпендикуляр на луч или нет:
Как же определить падает ли перпендикуляр на луч или нет? Если перпендикуляр не падает на луч, то угол $$MP1P2$$ – тупой иначе острый или прямой. Поэтому по знаку скалярного произведения векторов мы можем определить попадает ли перпендикуляр на луч или нет:
- $$(P1M, P1P2) < 0$$ - перпендикуляр не попадает на луч
- $$(P1M, P1P2) \ge 0$$ - перпендикуляр попадает на луч
Задача 19
Задача 20
Для прямой и окружности есть три варианта взаимного расположения: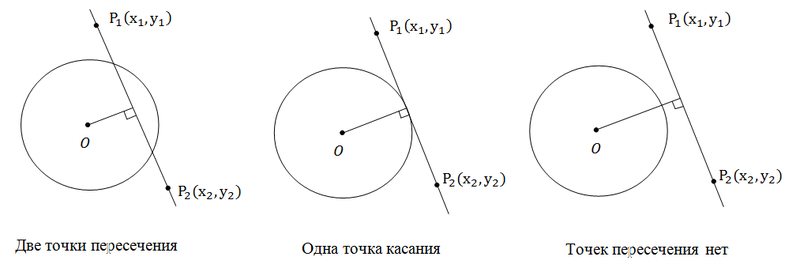 Мы имеем две точки пересечения, если расстояние от центра окружности до прямой меньше радиуса окружности. Одну точку касания, если расстояние от центра до прямой равно радиусу. И, наконец, ни одной точки пересечения, если расстояние от центра окружности до прямой больше радиуса окружности. Поскольку задача нахождения расстояние от точки до прямой была уже нами решена, то и эта задача тоже решена.
Мы имеем две точки пересечения, если расстояние от центра окружности до прямой меньше радиуса окружности. Одну точку касания, если расстояние от центра до прямой равно радиусу. И, наконец, ни одной точки пересечения, если расстояние от центра окружности до прямой больше радиуса окружности. Поскольку задача нахождения расстояние от точки до прямой была уже нами решена, то и эта задача тоже решена.