Сортировка вставками - одна из базовых сортировок. В общем случае работает достаточно медленно, однако очень эффективно сортирует почти упорядоченные массивы.
Алгоритм сортировки
Алгоритм заключается в том, что на i-ом проходе мы берём i-ый элемент (ключевой) и ставим его на свое место среди всех предыдущих. Для этого ключевой элемент запоминается во временную переменную, далее в левой (отсортированной) части массива, начиная с конца отрезка, перебираются элементы, которые сравниваются с ключевым. Если эти элементы больше ключевого, то они сдвигаются на одну позицию вправо, освобождая место для последующих элементов. Если в результате этого перебора попадается элемент, меньший или равный ключевому, то значит в текущую ячейку можно вставить ключевой элемент.
Визуализация алгоритма
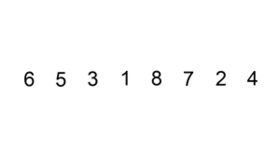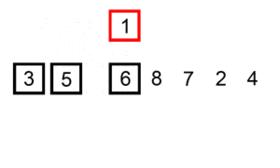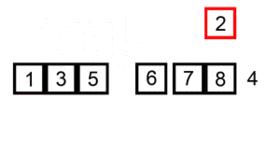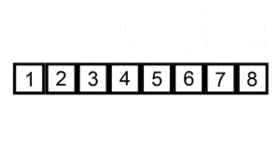
Модификации
Бинарные вставки. Вместо линейного поиска позиции будем использовать бинарный. Количество сравнений заметно уменьшится, но для того, чтобы поставить элемент на на своё место, всё равно будет необходимо переместить большое количество элементов. В итоге время выполнения алгоритма асимптотически не уменьшится. Бинарные вставки выгодно использовать только в случае когда сравнение занимает много времени по сравнению со сдвигом. Например когда мы используем массив длинных чисел.
Сортировка Шелла. Худшим вариантом входного массива для обычного алгоритма сортировки вставками является реверсно упорядоченный массив. Алгоритм сортировка Шелла обходит эту проблему.
Реализация алгоритма
static void InsertionSort (List<int> a)
{
for (int i = 0; i < a.Count; i++)
{
int j = 0;
while (a[j] < a[i]) j++;
int temp = a[i];
for (int k = i; k > j; k--)
{
a[k] = a[k - 1];
}
a[j] = temp;
}
}
Характеристики алгоритма
| Класс алгоритма | Сортировки вставками |
|---|---|
| Структура данных | массив |
| Худший случай | $$\mathcal{O}(n^2)$$ |
| Лучший случай | $$\mathcal{O}(n^2)$$ |
| средний случай | $$\mathcal{O}(n^2)$$ |
| Доп. затраты на память | $$\mathcal{O}(1)$$ |
| Устойчивость | да |