Решение рекуррентных соотношений
Многие алгоритмы имеют рекурсивную природу. При анализе таких алгоритмов, мы получаем рекуррентное соотношение, которое говорит о времени выполнения алгоритма. Мы получаем время выполнения алгоритма, как функцию зависящую от размера входных данных $$n$$. К примеру, для того, чтобы отсортировать массив сортировкой слиянием мы разбиваем его на два подмассивы длиной $$n/2$$ каждый и рекуррсивно их обрабатываем, а затем сливаем в один отсортированный массив. Временная сложность алгоритма сортировки слиянием имеет вид $$T(n) = 2T(n/2) + cn$$. Сюда можно отнести многие другие алгоритмы, например, быстрая сортировка, бинарный поиск, задачу о ханойских башнях, быстрое возведение в степень и так далее. Для нахождения времени работы рекурсивного алгоритма необходимо решить реккурентное соотношение (уравнение). Существует 3 основных способа решения таких уравнений.
Метод подстановки
Для решения рекуррентного уравнения данным методом необходимо выполнить два шага:
- сделать предположение о виде решения;
- с помощью метода математической индукции доказать верность предположения.
Данный метод позволяет находить как верхнюю оценку $$\mathcal{O}$$, так и нижнюю оценку $$\Omega$$.
Рассмотрим данный метод на ряде примеров.
Требуется решить следующее реккурентное соотношение $$T(n) = 2T(n/2) + n$$.
Предположим, что $$T(n) = \mathcal{O} (n\log n)$$, то есть $$T(n) \leq c \cdot n \log n$$. Докажем по индукции
- База индукции $$n=1$$, очевидно верно.
- Пусть соотношение верно для $$n/2$$. Покажем, что оно верно и для $$n$$:
$$ T(n) = 2 T\left(\dfrac{n}{2}\right) + n \leq 2\left(c \cdot \dfrac{n}{2} \cdot \log \left(\dfrac{n}{2}\right)\right) + n = cn\log \left(\dfrac{n}{2}\right) + n = cn\log n - cn + n \leq cn \log n = \mathcal{O} \left(n \log n\right)
$$
Данное соотношение верно, очевидно при $$c \geq 1$$. Аналогично, можно показать, что $$T(n) = \Omega(n\log n)$$.
Требуется решить следующее рекуррентное соотношение $$T(n) = 2T(\sqrt{n}) + \log n$$. Для решения такого уравнения сделаем подстановку $$n=2^m$$. Уравнение примет вид
$$T(2^m) = 2T(2^{m/2}) + m$$
Пусть $$S(m) = T(2^m)$$, тогда уравнение примет вид $$S(m) = 2S(m/2)+m = \mathcal{O} (m\log m)$$. Возвращаясь к исходной переменной имеем
$$T(n) = T(2^m) = S(m) = \mathcal{O} (m\log m) = \mathcal{O} (\log n \log \log n) $$.
Задача о Ханойских башнях. При решении классической задачи о ханойских башнях возникает рекуррентное уравнение
$$T(n) = 2T(n-1) + 1$$, при начальном условии $$T(0) = 0, \, T(1) = 1$$. Глядя на уравнение можно предположить, что решение имеет экспоненциальный вид. Действительно, вычисляя последовательно получим
$$T(2) = 3, \, T(3) = 7, \, T(4) = 15, \, T(5)=31, \ldots$$
Предполагаем, что $$T(n)=2^n - 1$$. Докажем верность данного утверждение методом математической индукции.
- База индукции $$n=1$$ очевидно верна.
- Предположим верность формулы для $$k=n-1$$ и покажем, что тогда формула верна и для $$k=n$$
$$T(n) = 2T(n-1) + 1 = 2(2^{n-1}-1) + 1 = 2^n -1$$
Таким образом формула верна и для $$k=n$$. Итак, $$T(n)=2^n - 1$$.
Числа Фибаначчи. Числа Фибонначи задаются рекуррентным уравнением $$Fn = F{n-1} + F_{n-2}$$ с начальными условиями $$F_0 = 0, \, F_1 = 1$$. Вычисляя последовательно получаем числа $$F_2 = 1, \, F_3 = 2, \, F_4 = 3, \, F_5 = 5, \, F_6 = 8, \ldots$$.По первым числам достаточно сложно угадать общую формулу для этих чисел. Сделаем предположение, что $$F_n \leq \alpha \cdot c^n$$, где $$\alpha > 0, \, c > 1$$. Имеем, индукционная гипотеза
$$Fn = F{n-1} + F_{n-2} \leq \alpha \cdot c^{n-1} + \alpha \cdot c^{n-2} \leq \alpha \cdot c^n$$
Последнее неравенство выполняется при $$c^n \geq c^{n-1} + c^{n-2}$$, то есть при $$c^2-c-1 \geq 0 $$. Наименьшее значение $$c$$ которое удовлетворяет данному неравенству это $$c = \phi = (1 + \sqrt{5})/2 \approx1.618034$$. Второй корень квадратного уравнения имеет меньшее абсолютное значение, так что мы можем его пропустить.
Итак, мы показали, что $$ F_n \leq \alpha \cdot \phi^n$$ для некоторой константы $$\alpha$$. Осталось показать верность для базы индукции.
$$\dfrac{F_0}{\phi^{0}} = \dfrac{0}{1} = 0, \quad \dfrac{F_1}{\phi^1} = \dfrac{1}{\phi} \approx 0.618034 > 0$$
Таким образом база индукции верна для $$\alpha \geq 1/\phi$$. Отсюда получаем $$F_n \leq \phi^{n-1}$$ для всех $$n$$. Аналогичным образом можно показать $$F_n \geq \beta \cdot \phi^n$$ для некоторой константы $$\beta$$, однако всем значениям $$n$$ удовлетворяет только $$\beta = 0$$! Если начать не с нулевого, а со второго члена $$F_2=1$$ в качестве базы индукции, то получим
$$ \dfrac{F_2}{\phi^2} = \dfrac{1}{\phi^2} \approx 0.381966 < \dfrac{1}{\phi}$$
Новая база индукции верна, при $$ \beta \leq \dfrac{1}{\phi^2}$$, откуда $$F_n \geq \phi ^{n-2}$$ для всех $$n \geq 1$$. Объединяя верхнюю и нижнюю оценку, получаем, что $$F_n = \Theta (\phi^n)$$. Точное замкнутое уравнение для последовательности чисел Фибоначчи имеет вид
$$F_n = \dfrac{\phi^n - (1-\phi)^n}{\sqrt{5}}$$
Метод итераций
Используя метод итерация мы итеративно раскрываем рекурсию шаг за шагом до тех пор пока не увидим общую закономерность. При использовании метода итераций не требуется делать предположения о виде решения, однако решение данным методом часто оказывается более сложным и грамоздким нежели с помощью подстановки (метода мат. индукции).
Рассмотрим ряд примеров.
Требуется решить рекуррентное уравнение $$T(n) = T(n - 1) + c, \, T(0) = 0$$. Раскроем $$k$$ раз рекурретное уравнение
$$T(n) = T(n-1)+c = T(n-2) + 2c = T(n-3)+3c = \ldots = T(n-k) + kc$$.
Итак, при $$n \geq k$$ имеем $$T(n) = T(n-k) + kc$$. Для остановки рекурсии, мы должны положить $$n=k$$, тогда $$T(n)=T(0)+cn=cn=\mathcal{O} (n)$$.
Требуется решить рекуррентное уравнение $$T(n)=T(n-1) + n, \, T(0) = 0$$. Аналогично предыдущему примеру, раскроем $$k$$ раз рекуррентное уравнение, получим
$$T(n) = T(n-1)+n = T(n-2) + n-1 + n = T(n-3) + n-2 + n-1 + n = \ldots \ = T(n-k) + (n-k+1) + \ldots + (n-3) + (n-2) + (n-1) + n = \sum_{i=n-k+1}^{n} i + T(n-k)$$
Для остановки рекурсии, положим $n=k$, тогда
$$T(n) = \sum_{i=1}^{n} i + T(0) = \dfrac{n(n+1)}{2} = \mathcal{O} (n^2)$$
Требуется решить рекуррентное уравнение $$T(n) = 2T\left( \dfrac{n}{2}\right) + c, \, T(1) = c$$. Раскроем $$k$$ раз рекурсию, получим
$$T(n) = 2T\left( \dfrac{n}{2}\right) + c = \ = 2 \left(2T\left(\dfrac{n}{4}\right) + c\right) + c = 2^2 T\left( \dfrac{n}{2^2}\right) + (2^2 - 1)c = \ = 2^2 \left(2 T\left(\dfrac{n}{8}\right) + c\right) + 3c = 2^3 T\left( \dfrac{n}{2^3}\right) + (2^3 - 1)c = \ \ldots \ = 2^k T\left( \dfrac{n}{2^k}\right) + (2^k - 1)c$$
Итак, при $$n \geq k$$ верно равенство $$T(n) = 2^k T\left( \dfrac{n}{2^k}\right) + (2^k - 1)c$$. Для остановки рекурсии, положим $$\dfrac{n}{2^k} = 1$$, то есть $$k=\log_2 n$$, тогда $$T(n) = 2^{\log_2 n} T(1) + (2^{\log_2 n} - 1)c = cn + (n-1)c = 2cn - c = \mathcal{O} (n)$$.
Метод итераций так же можно представить в виде рекурсивного дерева.
В этом методе мы рисуем рекуррентное дерево и рассчитываем время, затраченное на каждом уровне дерева. Наконец, мы суммируем работу, проделанную на всех уровнях. Чтобы нарисовать рекуррентное дерево, мы начинаем с верхнего уровня и спускаемся вниз, пока не найдем образец среди уровней. Шаблон обычно представляет собой арифметическую или геометрическую прогрессию.
Рассмотрим два примера
$$T(n) = 8T(n/2) + n^2, \, T(1) = 1$$
Запишем рекурсивное дерево следующим образом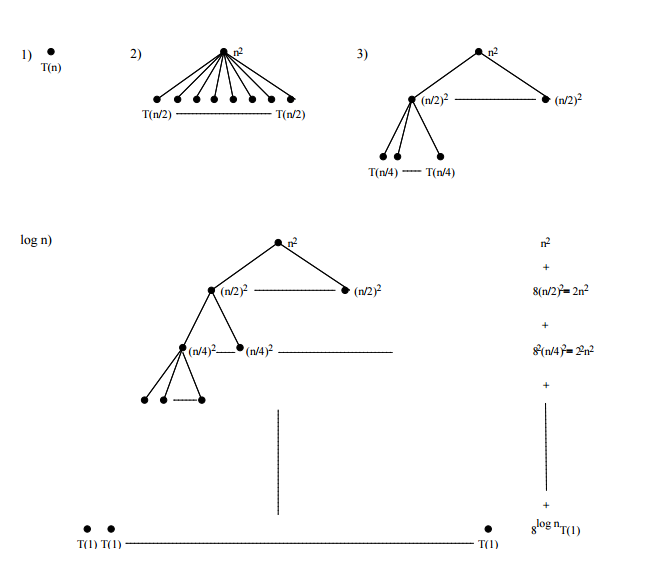
Имеем, $$T(n) = n^2 + 2n^2 + 2^2n^2 + 2^3n^2 + 2^4n^2 + \ldots + 2^{\log n−1}n^2 + 8^{\log2 n} = n^2 \sum{k=0}^{\log n - 1} 2^k + n^3$$
Первое слагаемое - это сумма геометрической прогрессии, имеем $$\sum_{k=0}^{\log n - 1} 2^k = \Theta(2^{\log n - 1}) = \Theta (n)$$. Таким образом $$T(n) = n^2 \Theta(n) + n^3 = \Theta(n^3)$$.
Пусть надо решить следующее рекуррентное уравнение $$T(n) = 3 T\left(\dfrac{n}{4} \right) + n, \, T(1) = 1$$.
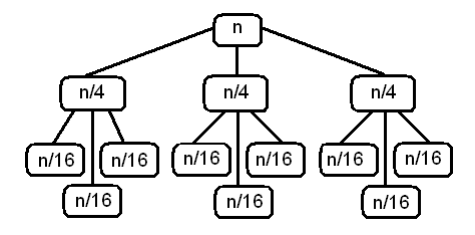
Суммиру все узлы получим сумму
$$n \left(1 + \dfrac{3}{4} + \dfrac{9}{16} + \ldots \right)$$
Поскольку высота дерева равна $$h = \log_4 n$$, то листьев будет $$3^{\log_4 n}$$. Итак, суммарная работа равна
$$T(n) = n \sum_{k=0} ^{\log_4 n - 1} \left(\dfrac{3}{4} \right)^k + 3^{\log_4 n} T(1) = 4n - 4 n^{\log_4 3} + n^{\log_4 3} < 4n = \mathcal{O}(n)$$
Рассмотрим еще один пример: пусть требуется решить рекуррентное уравнение $$T(n) = T\left(\dfrac{n}{4} \right) + T\left(\dfrac{n}{2} \right) + cn^2, \, T(1) = 1$$
Распишем дерево рекурсии
If we further break down the expression T(n/4) and T(n/2),
we get following recursion tree.
cn2
/ \
c(n2)/16 c(n2)/4
/ \ / \
T(n/16) T(n/8) T(n/8) T(n/4)
Breaking down further gives us following
cn2
/ \
c(n2)/16 c(n2)/4
/ \ / \
c(n2)/256 c(n2)/64 c(n2)/64 c(n2)/16
/ \ / \ / \ / \
Для того, чтобы найти значение $$T(n)$$, просуммируем значение каждого узла по уровням. получим следующую сумму
$$T(n) = c \left(n^2 + \dfrac{5}{16}n^2 + \dfrac{25}{256}n^2 + \ldots \right) = cn^2 \left(1 + \dfrac{5}{16} + \dfrac{25}{256} + \ldots \right)$$
Сумма в скобках - сумма бесконечно убывающей геометрической прогрессии со знаменателем $$q = \dfrac{5}{16}$$. Применяя формулу для суммы, находим $$T(n) = \dfrac{1}{1-\frac{5}{16}}n^2 = \mathcal{O} (n^2)$$
Основная теорема рекуррентных уравнений
Рекурсивный алгоритм решения многих задач может быть представлен в виде следующего псевдокода:
Функция T( n : размер задачи ) определена как:
if n < 1 then exit
Выполнить некоторое количество вычислений f(n)
T(n/b)
T(n/b)
...повторить a раз...
T(n/b)
конец функции
В приведенном примере алгоритм рекурсивно разделяет исходную задачу размера n на несколько новых подзадач, каждая размером n/b. Такое разбиение может быть представлено в виде дерева вызовов, в котором каждый узел соответствует рекурсивному вызову, а ветви, исходящие из узла — последующим вызовам для подзадач. Каждый узел будет иметь a ветвей. Также в каждом узле производится объём работы, соответствующий размеру текущей подзадачи n (переданному в данный вызов функции) согласно соотношению $$f(n)$$. Общий объём работы алгоритма определяется как сумма всех работ в узлах данного дерева.
Вычислительная сложность многих рекуррсвиных алгоритмов можем быть представлена следующим уравнением
$$ T(n) = aT\left(\dfrac{n}{b}\right) + n^c, \, a \geq 1, \, b\geq 1, \, c > 0
$$
Данное уравнение можно решить путём многократных подстановок выражения $${\displaystyle T\left({\frac {n}{b}}\right)}$$.
С помощью основной теоремы возможно быстрое вычисление подобных соотношений, что позволяет получить асимптотическую оценку времени работы рекурсивных алгоритмов в нотации $$\mathcal{O} (n)$$ ($$\Theta$$ - нотации), не производя подстановок.
В применении к анализу алгоритмов константы и функции обозначают:
- n — размер задачи.
- a — количество подзадач в рекурсии.
- n/b — размер каждой подзадачи. (Предполагается, что все подзадачи на каждом этапе имеют одинаковый размер.)
- f(n) — оценка сложности работы, производимой алгоритмом вне рекурсивных вызовов. В неё также включается вычислительная стоимость деления на подзадачи и объединения результатов решения подзадач.
Основная теорема рекуррентных уравнений: Пусть требуется решить рекуррентное уравнение $$T(n) = aT\left(\dfrac{n}{b}\right) + n^c, \, a \geq 1, \, b\geq 1, \, c > 0$$. Тогда
$$ T(n) =
\left{
\begin{aligned}
& \Theta(n^{\log_b a}), \quad a > b^c \\
& \Theta(n^c \log_b n), \quad a = b^c \\
& \Theta(n^c), \quad a < b^c \\
\end{aligned}
\right.
$$
Доказательство:
Изобразим дерево рекурсии для данного рекуррентного уравнения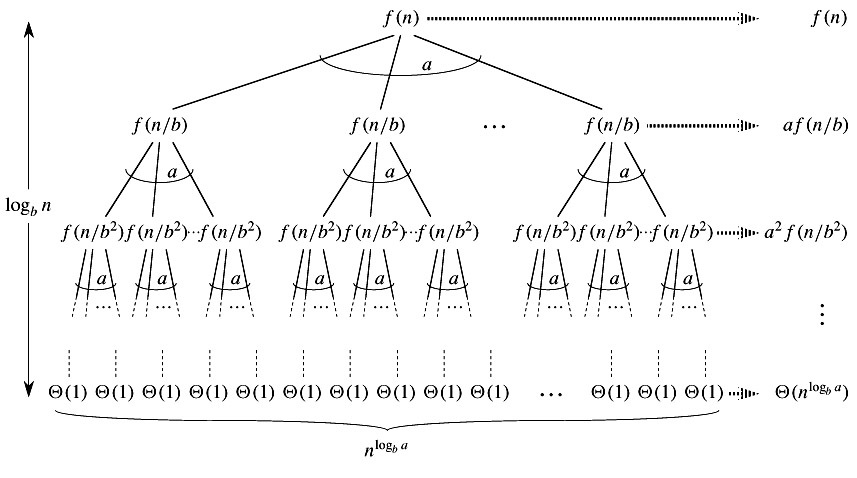
Применяя метод итераций получим
$$ T(n) = aT\left(\dfrac{n}{b} \right) + n^c = n^c + a \left( \left(\dfrac{n}{b} \right)^c +aT\left(\dfrac{n}{b^2} \right) \right) = n^c + \left(\dfrac{a}{b^c}\right)n^c + a^2T\left(\dfrac{n}{b^2}\right) = \ = n^c + \left(\dfrac{a}{b^c}\right)n^c + a^2 \left(\left(\dfrac{n}{b^2}\right)^c + aT\left(\dfrac{n}{b^3}\right) \right) = n^c + \left(\dfrac{a}{b^c}\right)n^c + \left(\dfrac{a}{b^c} \right)^2n^c + a^3T\left(\dfrac{n}{b^3}\right) = \ = \ldots = n^c + \left(\dfrac{a}{b^c}\right)n^c + \left(\dfrac{a}{b^c}\right)^2 n^c + \left(\dfrac{a}{b^c}\right)^3 n^c + \left(\dfrac{a}{b^c}\right)^4 n^c + \ldots + \left(\dfrac{a}{b^c}\right)^{\logb n - 1} n^c + a^{\log_b n}T(1) = \ = n^c \sum{k=0}^{\logb n - 1} \left(\dfrac{a}{b^c} \right)^k + a^{\log_b n} = n^c \sum{k=0}^{\log_b n - 1} \left(\dfrac{a}{b^c} \right)^k + n^{\log_b a}
$$
Поскольку
$$ \sum_{k=0}^{n} x^k = \left{ \begin{aligned} & \dfrac{x^{n+1} - x}{x - 1} = \Theta(x^n), \quad x > 1 \ & \dfrac{1}{1-x} = \Theta(1), \quad x < 1 \ \end{aligned} \right.
$$
Рассмотрим три случая
- $$a < b^c$$. В этом случае имеем
$$ a < b^c \iff \dfrac{a}{b^c} < 1 \Longrightarrow \sum{k=0}^{\log_b n - 1} \left(\dfrac{a}{b^c} \right)^k \leq \sum{k=0}^{+\infty} \left(\dfrac{a}{b^c} \right)^k = \dfrac{1}{1-\left(\dfrac{a}{b^c} \right)} = \Theta(1) \ a < b^c \iff \logb a < \log_b b^c = c \ T(n) = n^c \sum{k=0}^{\log_b n - 1} \left(\dfrac{a}{b^c} \right)^k + n^{\log_b a} = n^c \cdot \Theta(1) + n^{\log_b a} = \Theta(n^c)
$$
- $$a = b^c$$. В этом случае имеем
$$ a = b^c \iff \dfrac{a}{b^c} = 1 \Longrightarrow \sum{k=0}^{\log_b n - 1} \left(\dfrac{a}{b^c} \right)^k = \sum{k=0}^{\logb n - 1} = \Theta (\log_b n) \ a = b^c \iff \log_b a = \log_b b^c = c \ T(n) = \sum{k=0}^{\log_b n - 1} \left(\dfrac{a}{b^c} \right)^k + n^{\log_b a} = n^c \Theta(\log_b n) + n^{\log_b a} = \Theta(n^c \log_b n)
$$
- $$a > b^c$$. В этом случае имеем
$$ a>b^c \iff \dfrac{a}{b^c} > 1 \Longrightarrow \sum_{k=0}^{\log_b n - 1} \left(\dfrac{a}{b^c} \right)^{k} = \Theta \left(\left(\dfrac{a}{b^c} \right)^{\log_b n} \right) = \Theta \left(\dfrac{a^{\log_b n}}{(b^c)^{\log_b n}} \right) = \Theta\left(\dfrac{a^{\log_b n}}{n^c} \right) \ T(n) = n^c \cdot \Theta \left(\dfrac{a^{\log_b n}}{n^c} \right) + n^{\log_b a} = \Theta \left(n^{\log_b a} \right) + n^{\log_b a} = \Theta \left(n^{\log_b a} \right)
$$
Рассмотрим применение основной теоремы на практике.
Пример 1. Решим уравнение $$T(n) = 9T(n/3) + n$$. Имеем, $$a = 9, b = 3, c = 1, f(n) = n$$. Так как $$a > b^c$$, то мы попадаем под первый случай теоремы, значит $$T(n) = \Theta (n^{\log_b a}) = \Theta(n^2)$$.
Пример 2. Решим уравнение $$T(n) = T(2n/3) + 1$$. Имеем, $$a = 1, b=3/2, c = 0, f(n) = n^0 = \Theta(1)$$. Так как $$a=b^c$$, то мы попадаем под второй случай теоремы, значит $$T(n) = n^{0} \log_{1.5} n = \Theta(\log n)$$.
Пример 3. Решим уравнение $$T(n) = 2T(n/2) + n^2$$. ИМеем, $$a = 2, b = 2, c = 2, f(n) = n^2$$. Так как $$a < b^c$$, то мы попадаем под третий случай, значит $$T(n) = \Theta(n^c) = \Theta(n^2)$$.
Выражения не решаемые с помощью основной теоремы
Заметим, что с помощью основной теоремы могут быть решены далеко не все рекуррентные уравнения. Например, следующий уравнения не решаемы с помощью основной теоремы
- $$T(n) = 2^n T(n/2) + n^n$$. В данном случае $$a$$ не является константой, для основной теоремы требуется постоянное количество подзадач.
- $$T(n) = 2T(n/2) + \dfrac{n}{\log n}$$. В данном случае между $$f(n)$$ и $$\dfrac{n}{\log n}$$ существует неполиномиальная зависимость, поскольку $$\dfrac{f(n)}{n^{\log_b n}} = \dfrac{n}{n\log n} = \dfrac{1}{\log n} < n^{\varepsilon}$$ для любой константы $$\varepsilon > 0$$.
- $$T(n) = 0.5T(n/2) + n$$. В данном случае $$a<1$$, но основная теорема требует наличие хотя бы одной подзадачи.
- $$T(n) = 64T(n/8) - n^2\log n$$. В данном случае функция $$f(n)$$ является отрицательной величиной.
Некоторые рекуррентные уравнения
Сложности и рекуррентные уравнения некотороых алгоритмов
| Алгоритм | Рекуррентное уравнение | Время работы | Примечание |
|---|---|---|---|
| Бинарный поиск | $$T(n)=T(n/2) + \mathcal{O}(1)$$ | $$\mathcal{O}(\log n)$$ | |
| Последовательный поиск | $$T(n)=T(n - 1) + \mathcal{O}(1)$$ | $$\mathcal{O}(n)$$ | |
| Обход бинарного дерева | $$T(n)=2T(n/2) + \mathcal{O}(1)$$ | $$\mathcal{O}(n)$$ | |
| Алгоритм Штрассена | $$T(n)=7T(n/2) + \mathcal{O}(n^2)$$ | $$\mathcal{O}(n^{\log_2 7}) \approx \mathcal{O}(n^{2.81})$$ | |
| Сортировка выбором | $$T(n)=T(n-1) + \mathcal{O}(1)$$ | $$\mathcal{O}(n^2)$$ | |
| Сортировка слиянием | $$T(n)=2T(n/2) + \mathcal{O}(n)$$ | $$\mathcal{O}(n\log n)$$ | |
| Быстрая сортировка | $$T(n)=2T(n/2) + \mathcal{O}(1)$$ | $$\mathcal{O}(n\log n)$$ | |
| Выбор k-ой статистики (разбиение Quicksort) | $$T(n)=T(n/2) + \mathcal{O}(n)$$ | $$\mathcal{O}(n\log n)$$ | |
| Выбор k-ой статистики | $$T(n)=2T(n/2) + \mathcal{O}(1)$$ | $$\mathcal{O}(n)$$ |
