Худшее, среднее и лучшее время работы алгоритма

Выделяют три случая работы алгоритма

худший случай;
средний случай;
лучший случай.

Когда мы говорим, что время работы алгоритма равно $$T(n)$$, мы имеем в виду, что $$T(n)$$ является верхней границей времени выполнения, то есть имеет место для всех входных данных размера $$n$$. Это называется анализом наихудшего случая. Алгоритм может работать значительно быстрее на некоторых размерах входных данных $$n$$, но это не имеет значения при оценке худшего случая. Если на выполнение алгоритма требуется $$T(n) = cn^2+k$$ шагов хотя бы для одного входного значения $$n$$ и $$T(n) = cn+k$$ шагов на всех остальных входных данных, мы все равно говорим, что алгоритм является квадратным, то есть в худшем случае работает за время пропорциональное $$n^2$$. Нужно понимать, что знание сложности алгоритма в худшем случае является очень важным, так как имеет решающее значение в возможности применения данного алгорит

Популярная альтернатива анализу наихудшего случая - анализ среднего случая. Здесь мы не пытаемся найти худший случай времени выполнения, а попытаться вычислить ожидаемое время, затраченное на случайно выбранных входных данных. Такой анализ, как правило, сложнее, так как он включает в себя вероятностные рассуждения и часто требует знания о распределении входных данных. С другой стороны, он может быть более полезным, потому что иногда наихудший случай алгоритма является обманчиво плохим. Хорошим примером этого, является популярный алгоритм быстрой сортировки, время работы которого в худшем случае на массиве длины $$n$$ пропорциональное $$n^2$$, однако ожидаемое в среднем время работы пропорциональное $$n\log n$$.

Намного меньше информации об алгоритме может сказать оценка наилучшего случая.

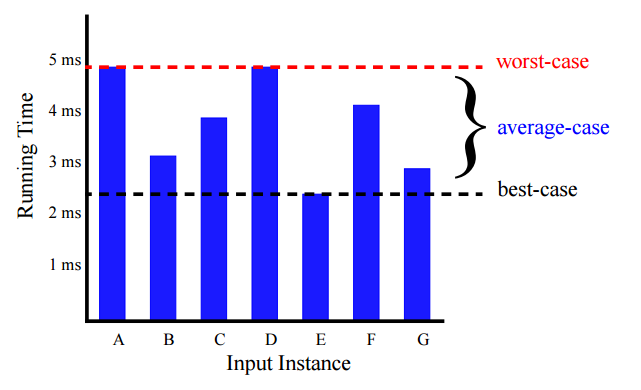
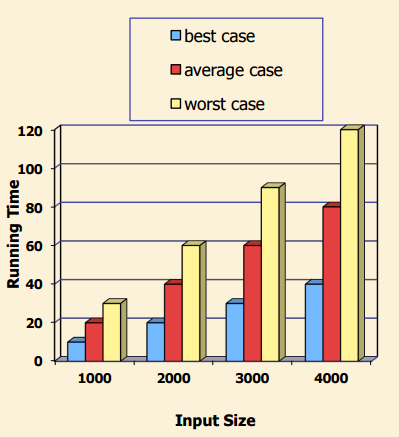
Рассмотрим какую сложность в каждом из трех случаев имеет последовательный поиск элемента в массиве.

int LinearSearch(int[] arr, int x)
{
  for (int i = 0; i < a.Length; i++)
  {
   if (arr[i] == x)
     return i;
  }
  return -1;
}

Худший случай

В худшем случае анализа, мы вычислим верхнюю границу времени работы алгоритма. Мы должны знать, случай, на котором выполняется максимальное количество выполняемых операций. Для линейного поиска, худшим случаем является поиск отсутсвующего в массиве элемента. В данном случае алгоритм сравнит каждый элемент массива с искомым элементом. Таким образом, в худшем случае временная сложность линейного поиска будет $$\Theta(n)$$, то есть алгоритм имеет линейный порядок, пропорциональный размеру входного массива.

Средний случай

При анализе сложности алгоритма в среднем случае, мы рассматриваем все возможные исходы входных данных и рассчитываем время вычисления для каждого из исходов. Для нахождения среднего значения поделим просто сумму на количество входов. Для анализа в среднем нам нужно знать распределение входных данных. Предположим, что в задаче линейного поиска все входные данные распределены равномерно (включая случай когда поиск осуществляется по отсутствующему элементу). Получаем среднюю сложность алгоритма

$$ Average = \dfrac{\sum_{n=1}^{n+1} \Theta(i)}{n + 1} = \dfrac{\Theta((n+1)\cdot (n+2)/2)}{n + 1} = \Theta (n)

Лучший случай

При анализе сложности алгоритма в лучшем случае, мы вычисляем нижнюю границу времени работы алгоритма. Мы должны знать случай, на котором выполянется минимальное количество операций. В случае с линейным поиском, лучший случаем является поиск самого первого элемента в массиве. В таком случае количество затраченных операций будет всегда константным, то есть не будет зависеть от размера входного массива. Таким образом, сложность алгоритма линейного поиска в лучшем случае равна $$\Theta (1)$$.

В большинстве случаев, мы исследуем алгоритм на худшую оценку. В таком случае мы гарантируем, что время работы алгоритма не будет превосходить некоторого числа, что является хорошей информацией. Нахождение сложности алгоритма в среднем не является столь простой задачей, поскольку мы должны знать математическое распределение для всех возможных входных данных. Сложность алгоритма в лучшем случаем мало чем помогает при реальной оценке времени работы алгоритма. Таким образом алгоритм может в лучшем случае работать секунды, а в худшем случае дни и даже годы.

Для некоторых алгоритмов все три случая сложности совпадают. Например, сортировка слиянием в лучшем, среднем и худшем случае имеет сложность $$\Theta (n \log n)$$. Однако один из самых быстрых алгоритмов сортировки на практике - быстрая сортировка, имеет в худшем случае (массив уже отсортирован) квадратичную сложность работы, при выборе разделяющего элемента последним в массиве. Для сортировки вставками, наихудший случай достигается когда массив отсортирован в обратном порядке, а наилучший когда массив уже отсортирован в нужном порядке.

Худшее, среднее и лучшее время работы алгоритма