Интерполяционный поиск (интерполирующий поиск) основан на принципе поиска в телефонной книге или, например, в словаре. Вместо сравнения каждого элемента с искомым, как при линейном поиске, данный алгоритм производит предсказание местонахождения элемента: поиск происходит подобно двоичному поиску, но вместо деления области поиска на две части, интерполирующий поиск производит оценку новой области поиска по расстоянию между ключом и текущим значением элемента. Другими словами, бинарный поиск учитывает лишь знак разности между ключом и текущим значением, а интерполирующий ещё учитывает и модуль этой разности и по данному значению производит предсказание позиции следующего элемента для проверки. В среднем интерполирующий поиск производит log(log(N)) операций, где N есть число элементов, среди которых производится поиск. Число необходимых операций зависит от равномерности распределения значений среди элементов. В плохом случае (например, когда значения элементов экспоненциально возрастают) интерполяционный поиск может потребовать до O(N) операций.

Interpolation search is a modification of binary search, where additional information about the data is used to achieve better time complexity.

Разбиение использущее линейное распределение данных

Отличие заключается в том, что алгоритмы вроде двоичного поиска не делают различий между "немного больше" и "существенно больше".

So the interpolation search is based on some simple facts. The binary search divides the interval on two equal sub-lists, as shown on the image bellow.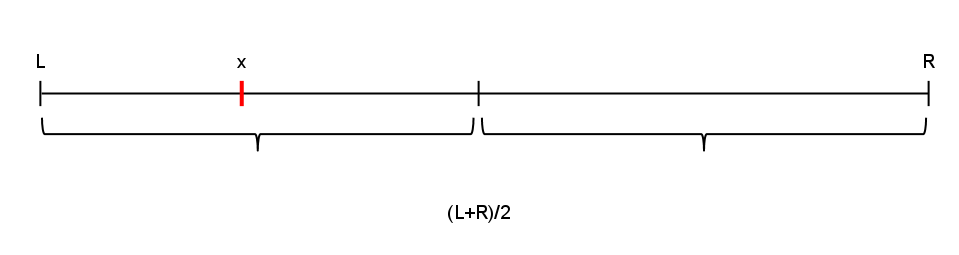

The binary search algorithm divides the list in two equal sub-lists!

What will happen if we don’t use the constant ½, but another more accurate constant “C”, that can lead us closer to the searched item.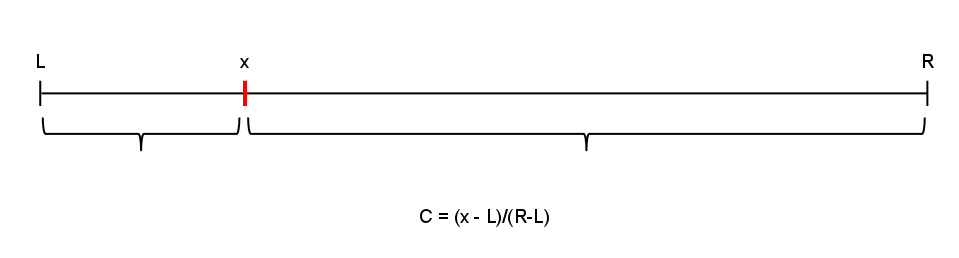

The question is how to find this value? Well, we know bounds of the interval and looking closer to the image above we can define the following formula.

$$ C =(x-L)/(R-L)

Пусть — отсортированный массив изчисел, — значение, которое нужно найти. Поиск происходит подобно двоичному поиску, но вместо деления области поиска на две примерно равные части, интерполирующий поиск производит оценку новой области поиска по расстоянию между ключом и текущим значением элемента. Если известно, чтолежит между $a\_l$ и $a\_r$ , то следующая проверка выполняется примерно на расстоянии $\frac{x - a\_l}{a\_r - a\_l} \cdot$ $r - l$ от.

Формула для разделительного элементаполучается из следующего уравнения: $\frac{x - a\_l}{m - l} = \frac{a\_r - a\_l}{r - l}$ — откуда следует, что $\frac{x - a\_l}{a\_r - a\_l} \cdot$ $r - l$ . На рисунке внизу показано, из каких соображений берется такая оценка. Интерполяционный поиск основывается на том, что наш массив представляет из себя что-то наподобии арифметической прогрессии.

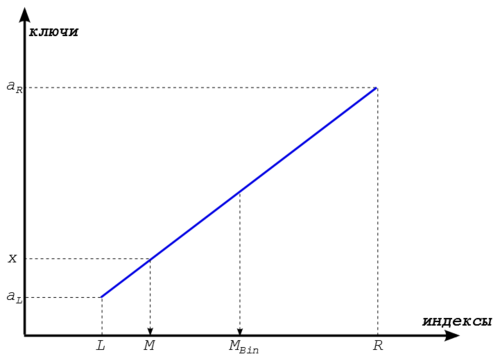
Таким образом алгоритм интерполяционного поиска можно записать следущим образом:

Описание алгоритма

Step 1 − Start searching data from middle of the list.
Step 2 − If it is a match, return the index of the item, and exit.
Step 3 − If it is not a match, probe position.
Step 4 − Divide the list using probing formula and find the new midle.
Step 5 − If data is greater than middle, search in higher sub-list.
Step 6 − If data is smaller than middle, search in lower sub-list.
Step 7 − Repeat until match.

Algorithm
Rest of the Interpolation algorithm is same except the above partition logic.

Step1:In a loop, calculate the value of “pos” using the probe position formula.
Step2:If it is a match, return the index of the item, and exit.
Step3:If the item is less than arr[pos], calculate the probe position of the left sub-array. Otherwise calculate the same in the right sub-array.
Step4:Repeat until a match is found or the sub-array reduces to zero.

Визуализация работы алгоритма

Реализация алгоритма

    // Возвращает индекс элемента со значением toFind или -1, если такого элемента не существует
    int mid;
    int low = 0;
    int high = sortedArray.length - 1;

    while (sortedArray[low] < toFind && sortedArray[high] > toFind) {
        mid = low + ((toFind - sortedArray[low]) * (high - low)) / (sortedArray[high] - sortedArray[low]);

        if (sortedArray[mid] < toFind)
            low = mid + 1;
        else if (sortedArray[mid] > toFind)
            high = mid - 1;
        else
            return mid;
    }

    if (sortedArray[low] == toFind)
        return low;
    else if (sortedArray[high] == toFind)
        return high;
    else
        return -1; // Not found
}

Производительность и анализ сложности

Асимптотически интерполяционный поиск превосходит по своим характеристикам бинарный. Если ключи распределены случайным образом, то за один шаг алгоритм уменьшает количество проверяемых элементов сдо $\sqrt n$ [1]. То есть, после-ого шага количество проверяемых элементов уменьшается до $n^{\frac{1}{2^k}}$ . Значит, остаётся проверить только 2 элемента (и закончить на этом поиск), когда $\frac{1}{2^k} = \log\_{n}2 = \frac{1}{\log\_{2}n}$ . Из этого вытекает, что количество шагов, а значит, и время работы составляет $O$\log \log n$$ .

При "плохих" исходных данных (например, при экспоненциальном возрастании элементов) время работы может ухудшиться до $O$n$$ .

Эксперименты показали, что интерполяционный поиск не настолько снижает количество выполняемых сравнений, чтобы компенсировать требуемое для дополнительных вычислений время (пока таблица не очень велика). Кроме того, типичные таблицы недостаточно случайны, да и разница между значениями $\log \log n$ и $\log n$ становится значительной только при очень больших. На практике при поиске в больших файлах оказывается выгодным на ранних стадиях применять интерполяционный поиск, а затем, когда диапазон существенно уменьшится, переходить к двоичному.

If we make no assumptions about the distribution of keys in arr, interpolation search is O(N) for an array of size N,since the array may have an exponential distribution of keys. However if the keys are in a uniform distribution, interpolation search is O(log log N).

Like most of computer science, Interpolation search involves a trade-off. We increase the amount of computation involved in each step in the hope of decreasing the number of steps.

This may be useful when data access is costly, say,when you have an unindexed, sorted array on a disk, and you must find a key.

And lastly the most important point. While most resources you might find explain interpolation search, assuming a uniform distribution, it is not necessary. The idea of interpolation search is much more powerful than that!

As an example, if you know that the distribution of keys is exponential, you may calculate mid as

mid = low + ((key - log(arr[low])) * (high - low)) / (log(arr[high]) - log(arr[low]))

The complexity of this algorithm is log2(log2(n)) + 1. While I wont cover its proof, I’ll say that this is very slowly growing function as you can see on the following chart.

$log$n$ compared to log$log\(n$\)$

Indeed when the values are equally dispersed into the interval this search algorithm can be extremely useful – way faster than the binary search. As you can see log2(log2(100 M)) ≈ 4.73 !!!

Оптимизации

Характеристики алгоритма

Класс алгоритма	Алгоритм поиска
Структура данных	отсортированный массив
Худший случай	$$\mathcal{O}(n)$$
Лучший случай	$$\mathcal{O}(\log (\log n))$$
Средний случай	$$\mathcal{O}(\log (\log n))$$ в случае равномерного распределения ключей и $$\mathcal{O}(n)$$ в противном случае
Затраты на память	$$\mathcal{O}(1)$$

Приложение и задачи решаемые с помощью интерпояционного поиска

As I said already this algorithm is extremely interesting and very appropriate in many use cases. Here’s an example where interpolation search can be used. Let’s say there’s an array with user data, sorted by their year of birth. We know in advance that all users are born in the 80’s. In this case sequential or even binary search can be slower than interpolation search.$list = array(

0 =&gt; array\('year' =&gt; 1980, 'name' =&gt; 'John Smith', 'username' =&gt; 'John'\),

1 =&gt; array\('year' =&gt; 1980, ...\),

...

10394 =&gt; array\('year' =&gt; 1981, 'name' =&gt; 'Tomas M.', ...\),

...

348489 =&gt; array\('year' =&gt; '1985', 'name' =&gt; 'James Bond', ...\),

...

2808008 =&gt; array\('year' =&gt; '1990', 'name' =&gt; 'W.A. Mozart', ...\)

);

Now if we search for somebody born in 1981 a good approach is to use interpolation search.

Преимущества и недостатки

When all elements in the list are sorted and evenly distributed, then executing time of Interpolation search algorithm is

log(log n) ie Best case.
However, When the elements in the list are increased exponentially, then executing time of Interpolation search algorithm is

0(n) ie Worst case.

Interpolation search, also called as extrapolation search.

Interpolation searching algorithm is only used when the elements in an array is sorted and evenly distributed.

Interpolation search algorithm is the combination of both binary search algorithm and linear search algorithm.

The working of interpolation search algorithm is very much similar to our brain on look for the name Manish in the telephone directory, we know that it will be near the extreme left, So if we tend to apply binary search algorithm to dividing the list in two halves each time will lead to worst case. Thus we need to divide the telephone directory into two half for the first time (binary search algorithm) and start search from the first occurance of letter M using linear search algorithm.

На практике интерполяционный поиск часто быстрее бинарного, так как с вычислительной стороны их отличают лишь применяемые арифметические операции: интерполирование — в интерполирующем поиске и деление на два — в двоичном, а скорость их вычисления отличается незначительно, с другой стороны интерполирующий поиск использует такое принципиальное свойство данных, как однородность распределения значений. Ключом может быть не только номер, число, но и, например, текстовая строка, тогда становится понятна аналогия с телефонной книгой: если мы ищем имя в телефонной книге, начинающееся на «А», следовательно, нужно искать его в начале, но никак не в середине. В принципе, ключом может быть всё что угодно, так как те же строки, например, запросто кодируются посимвольно, в простейшем случае символ можно закодировать значением от 1 до 33 (только русские символы) или, например, от 1 до 26 (только латинский алфавит) и т. д.

Obviously, to do an interpolation search, you need some type of key for which more than ordering is known -- you have to be able to do computations on the keys to estimate a likely distance, not just compare keys to determine which is greater or lesser.

As far as properties of the dataset go, it mostly comes to one property: a likelihood that the keys are_reasonably_evenly (or at least predictably) distributed throughout the range of possibilities. Without that, an interpolation search can actually be_slower_than a binary search.

For example, consider a data set with strings of lower-case letters as keys. Let's assume you have a key that starts with "x". An interpolation search will clearly indicate that you should start searching very close to the end of the set. If, however,_most_of your keys actually start with 'z', and almost none with anything from 'a' though 'y', the one you're searching for may actually be very close to the beginning of the set instead. It can/may take a considerable number of iterations before the search gets close to the beginning where the string starting with 'w' reside. Each iteration would remove only ~10% of the data set from consideration, so it would take several iterations before it got close to the beginning where the keys starting with 'w' actually reside.

By contrast, a binary search would_start_at the middle, get to the one-quarter mark at the second iteration, one-eighth mark on the third, and so on. Its performance would be nearly unaffected by the skew in the keys. Each iterations would remove half the data set from consideration, just as if the keys were evenly distributed.

I hasten to add, however, that it really does take_quite_a skewed distribution to make an interpolation search noticeably worse than a binary search. It can, for example, perform quite well even in the presence of a fair amount of localized clustering.

I should also mention that an interpolation search does not necessarily need to use linear interpolation. For example, if your keys are known to follow some non-linear distribution (e.g., a bell-curve), it becomes fairly easy to take that into account in the interpolation function to get results little different from having an even distribution.