Асимтотические нотации

При оценке времени работы алгоритма сортировки вставками со сложностью $$T(n) = cn^2+k$$, мы не знаем, чему равны константы $$c, \, k$$. Мы знаем, что эти константы достаточно умеренного размера, но на деле это не имеет большого значения, поскольку у нас есть достаточно доказательств из асимптотического анализа, чтобы сказать, что сортировка слиянием (MergeSort) работает быстрее, хотя константы могут несколько отличаться.

Мы не всегда в состоянии измерить константу $$c$$ непосредственно. Например, мы можем знать, что количество машиных инструкций (команд) требуемых для выполнения данного выражение, (например, конструкция if), является константным но мы не можем точно знать чему оно ровно. Кроме того, одна и та же последовательность команд, выполняемых на Intel Core i 7 будет занимать меньше времени, чем на Pentium II. Таким образом, эти оценки, как правило производятся, с точностью до постоянного множителя. По этим причинам, мы обычно игнорируем постоянные множители при измерении асимптотического времени работы алгоритма.

Компьютерные ученые разработали удобные обозначения для сокрытия постоянных множителей. Мы пишем $$\mathcal{O} (n)$$ (порядка $$n$$) вместо $$cn$$ для некоторой константы $$c$$. Таким образом, алгоритм имеет порядок $$O(n)$$ иначе говоря выполняется за линейное время, если существует фиксированная константа $$c$$, такая что, для любых достаточно больших $$n$$, время работы алгоритма занимает время $$cn$$ на входных данных размера $$n$$. Алгоритм имеет порядок $$\mathcal{O} (n^2)$$, то есть выполняется за квадратичное время, если существует константа $$c$$, такая что для всех достаточно больших $$n$$, алгоритм занимает времени не больше, чем $$cn^2$$ на входных данных размера $$n$$. Выражение $$\mathcal{O}(1)$$ означает, константное время, которое не зависит от размера входных данных $$n$$.

Полиномиальное время означает $$n^{\mathcal{O} (1)}$$ или, что то же самое $$n^c$$, для некоторой константы $$c$$. Таким образом, любой константный, линейный или кубический алгоритм является полиномиальным.

$$\mathcal{O}$$ нотация лаконично отражает существенные различия в асимптотических темпах роста функций.

Одним из важных преимуществ $$\mathcal{O}$$ нотации является то, что она позволяет анализировать алгоритмы гораздо проще, так как мы можем игнорировать слагаемые более низкого порядка. Например, алгоритм, который работает во времени

$$ T(n) = 10n^3 + 24n^2 + 3n \log n + 144

является по прежнему кубическим, поскольку

$$ 10n^3 + 24n^2 + 3n \log n + 144 \leq 10n^3 + 24n^3 + 3n^3 + 144n^3 \leq (10 + 24 + 3 + 144)n^3 = \mathcal{O}(n^3)

Конечно, так как мы игнорируем постоянные множители, любые два линейных алгоритмы будут считаться одинаково хорошими с точки зрения асимтотического анализа. Может случиться даже так, что константа окажется настолько большой в линейном алгоритме, что даже экспоненциальный алгоритм с малой константой может быть предпочтительным на практике. Это действительная слабое место асимптотического анализа и $$\mathcal{O}$$ нотации, однако, на практике такое встречается редко. Просто надо понимать, что асимптотически оптимальный алгоритм не обязательно является лучшим вариантом.

Следующие асомтотические порядки встречаются достаточно часто при оценке времени работы алгоритмов

Порядок роста	Название
$$\mathcal{O}(1)$$	константный
$$\mathcal{O}(\log n)$$	логарифмический
$$\mathcal{O}(n)$$	линейный
$$\mathcal{O}(n\log n)$$	квазилинейный
$$\mathcal{O}(n^2)$$	квадратичный
$$\mathcal{O}(n^3)$$	кубический
$$n^{\mathcal{O}(1)} = n^c$$	полиномиальный
$$2^{\mathcal{O}(n)}$$	экспоненциальный

Как уже было сказано выше, основная идея асимтотического анализа - это измерение эффективности алгоритма, которая не зависит от конкретных машиных констант. В асимптотическом анализе приняты следующие 3 обозначения которые используются для определения сложности алгоритмов.

Нотация $$\Theta$$

Пусть $$f(n)$$ и $$g(n)$$ — положительные функции положительного аргумента, $$n \geq 1$$ (количество объектов на входе и количество операций — положительные числа), тогда:

$$f(n) = \Theta(g(n))$$, если существуют положительные константы $$c_1, c_2$$ и $$n_0$$, такие, что: $$c_1 \cdot g(n) \leq f(n) \leq c_2 \cdot g(n)$$, при $$n \geq n_0$$.

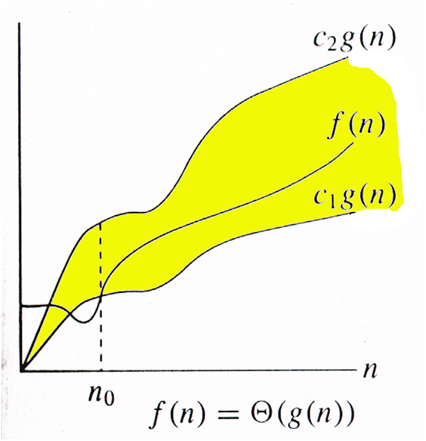
Обычно говорят, что при этом функция $$g(n)$$ является асимптотически точной оценкой функции $$f(n)$$, так как по определению, функция $$f(n)$$ не отличается от функции $$g(n)$$ с точностью до постоянного множителя.

Отметим, что из того, что $$f(n) = Θ(g(n))$$ следует, что $$g(n) = Θ(f(n))$$.

Рассмотрим следущие примеры:

$$f(n) = 3n^3+4n^2+n+100$$. Имеем $$f(n) = \Theta (n^3)$$, поскольку верно следующее неравенство $$n^3 \leq 3n^3+4n^2+n+100 \leq 5n^3$$ с константами $$c_1=1, \, c_2 = 5, \, n_0=5$$.
$$f(n)=4n^2 + n \ln n + 170$$. Имеем $$f(n)= Θ(n^2)$$, поскольку верно следующее неравенство $$n^2 \leq 4n^2 + n \ln n + 170 \leq 10n^2$$ с константами $$c_1=1, \, c_2=10, \, n_0=7$$.

Запись $$f(n)=Θ(1)$$ — означает, что $$f(n)$$ или равна константе, не равной нулю, или $$f(n)$$ ограничена константой на бесконечности, например $$f(n) = 10+\dfrac{7}{n} = Θ(1)$$, так как ограничена константой 17.

Нотация $$\mathcal{O}$$

В отличие от оценки $$Θ$$, оценка $$\mathcal{O}$$ требует только, что бы функция $$f(n)$$ не превышала $$g(n)$$ начиная с некоторого $$n > n_0$$, с точностью до постоянного множителя.

$$ f(n) = \mathcal{O} (g(n))$$ если существует положительная константа $$c$$ и $$n$$, такие, что: $$0 \leq f(n) \leq c \cdot g(n)$$, при $$n \geq n_0$$.

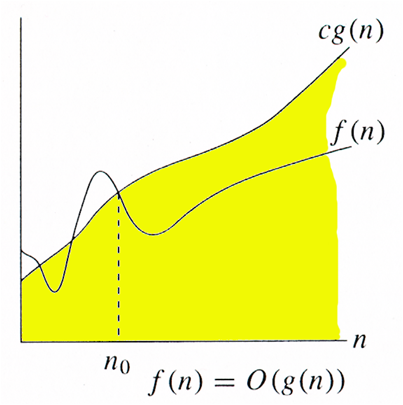
Другими словами запись $$f(n)=\mathcal{O}(g(n))$$ означает, что отношение $$\dfrac{f(n)}{g(n)}$$ ограниченно сверху некоторой константой.

Например, для всех функций $$f(n)=\dfrac{3}{n}, \, f(n)= 120, \, f(n)=7n+20, \, f(n)=n\ln (n), \, f(n)=10n^2+4n+7$$ будет справедлива оценка $$\mathcal{O} (n^2)$$. Указывая оценку $$\mathcal{O}$$, есть смысл указывать наиболее "близкую" мажорирующую функцию.

К примеру рассмотрим сортировку вставками. Мы знаем, что в лучшем случае (массив уже отсортирован в правильном порядке) сложность алгоритма является линейной, а в среднем и худшем случаях сложность является квадратной. В этом случае мы можем сказать, что сложность алгоритма сортировки вставками есть $$\mathcal{O}(n^2)$$. То есть это покрывает и лучший случай работы алгоритма, когда сложность является линейной. В случае ели бы мы пользовались $$\Theta$$ нотацией, нам пришлось бы разбивать ответ на два случая:

В худшем случае сложность алгоритма сортировки вставками равна $$\Theta(n^2)$$;
В лучшем случае сложность алгоритма сортировки вставками равна $$\Theta(n)$$.

Нотация $$\mathcal{O}$$ удобна когда нам необходимо найти только верхнюю границу времени выполнения алгоритма. Как правило верхняя граница находится достаточно легко, просто посмотрев на псевдокод алгоритма.

Полезные правила $$\mathcal{O}$$ нотации

Если $$f(n)=a_0+a_1n+a_2n^2+\ldots + a_kn^k$$ - многочлен степени $$k$$, то $$f(n) = \mathcal{O} (n^k)$$
Если $$d(n) = \mathcal{O} (f(n))$$ и $$e(n)=\mathcal{O} (g(n))$$, то
- $$d(n) + e(n) = \mathcal{O} (f(n) + g(n))$$
- $$d(n) \cdot e(n) = \mathcal{O} (f(n) \cdot g(n))$$
Если $$d(n) = \mathcal{O} (f(n))$$ и $$f(n) = \mathcal{O} (g(n))$$, то $$d(n) = \mathcal{O} (g(n))$$
$$cn^m = \mathcal{O}(n^k)$$ для любой константы $$c$$ и произвольных $$m \leq k$$
$$\mathcal{O}(cf(n)) = \mathcal{O}(f(n))$$ для любой константы $$c > 0$$
$$c = \mathcal{O}(1)$$ для любой константы $$c > 0$$
$$\log_b n = \mathcal{O}(\log n)$$ для любого основания $$b$$ логарифма

Все эти правила за исклчением 4 верны и для $$\Theta$$ нотации.

Рассмотрим следущие примеры:

$$f(n) = 7n-2$$. Имеем, $$f(n)= \mathcal{O}(n)$$, поскольку верно следущее неравенство $$f(n) \leq cn$$, где $$c = 7, \, n_0 = 1$$;
$$f(n) = 3n^3 + 20n^2+5$$. Имеем, $$f(n) = \mathcal{O}(n^3)$$, поскольку $$f(n) \leq cn^3$$, где $$c =4, \, n_0 = 21$$;
$$f(n) = 3\log_2 n + 5$$. Имеем, $$f(n) = \mathcal{O}(\log_2 n)$$, поскольку $$f(n)\leq c\log_2 n$$, где $$c = 8, \, n_0 = 2$$.

Нотация $$\Omega$$

Подобно тому, как $$\mathcal{O}$$ нотация показывает верхнюю оценку сложности алгоритма, нотация $$\Omega$$ показывает асимтотическую нижнюю границу. Данная нотация может быть полезна когда мы исследуем лучшую оценку работы алгоритма. Как уже говорилось выше, лучшая оценка работы алгоритма не сообщает как правило никакой полезной информации для исследования сложности работы алгоритма, в следствии чего данная нотация является наименее используемой среди всех трех.

$$f(n) = \Omega(g(n))$$ если существует положительная константа $$c$$ и $$n_0$$, такие, что: $$0 \leq c\cdot g(n) \le f(n)$$, при $$n \geq n_0$$.

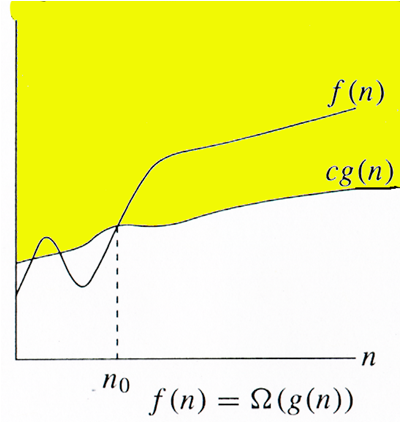
Возвращаясь к алгоритму сортировки вставками, мы можем сказать, что его сложность равна $$\Omega(n)$$, однако это не очень полезная информация о данном алгоритме, посколько нас интересут как правило средний и худший случай.

Асимптотическое обозначение $$\mathcal{O}$$ восходит к учебнику Бахмана по теории простых чисел (Bachman, 1892), обозначения $$\Theta, \, \Omega$$ были введены Дональдом Кнутом (Donald Knuth).

Отметим, что не всегда для пары функций справедливо одно из асимптотических соотношений, например для $$f(n)=n^{1+\sin n}$$и $$g(n)=n$$ не выполняется ни одно из асимптотических соотношений.

Интуитивное понимание нотаций

Название	Обозначение	Понимание
Тетта большое	$$f(n) = \Theta (g(n))$$	$$f=g$$ с точностью до константы, то есть $$f$$ и $$g$$ имеют одинаковый порядок роста
О большое	$$f(n) = \mathcal{O}(g(n))$$	$$f\leq g$$ с точностью о константы, то есть $$f$$ растет не быстрее чем $$g$$
Омега большое	$$f(n) = \Omega (g(n))$$	$$f \geq g$$ с точностью о константы, то есть $$f$$ растет не медленнее чем $$g$$