Примитивные операции

Под примитивными операциями подразумевается низкоуровневые операции которые в большинстве случаев не зависят от языка программирования, могут быть легко записаны на псевдокоде, а так же выполнятся за константное время. К примитивным операциям относятся следующие

• вызов функции;
• возвращение значения из функции;
• выполнение простейших арифметических операций (+, -, *, /);
• сравнение двух чисел;
• присвоение значения переменной;
• обращение по индексу массива;
• и т.д.

Рассмотрим алгоритм нахождения наибольшего элемента в массиве и посчитаем количество совершаемых в нем примитивных операций.

public int ArrayMax(int[] a)               // Количество операций
{
  int max = a[0];                          // 2

  for (int i = 1; i < n; i++)              // 2n
  {
    if (a[i] > max)                        // 2(n-1)
      max = a[i]                           // 2(n-1)
  }

  return max;                              // 1
}
                                           // Общее количество примитивных операций: 6n-1

Максимальное количество примитивных операций совершаемых алгоритмом равно $$6n-1$$. Пусть $$a$$ - время за которое выполняется самая быстрая операция, $$b$$ - время за которое выполняется самая медленная операция. Пусть $$T(n)$$ время выполнения алгоритма в наихудшем случае. Тогда

$$ a(6n-1) \leq T(n) \leq b(6n-1)

$$ Таким образом время $$T(n)$$ заключено между двумя линейными функциями. Изменение программного или аппаратного обеспечения, влияет только на постоянный множитель в $$T(n)$$, но качественно не изменяет скорость роста $$T(n)$$.

Линейная скорость роста времени $$T(n)$$ является внутренним свойством алгоритма нахождения максимального элемента в массиве.

На следущей картинке изображено время выполнения примитивных операций на современном компьтере.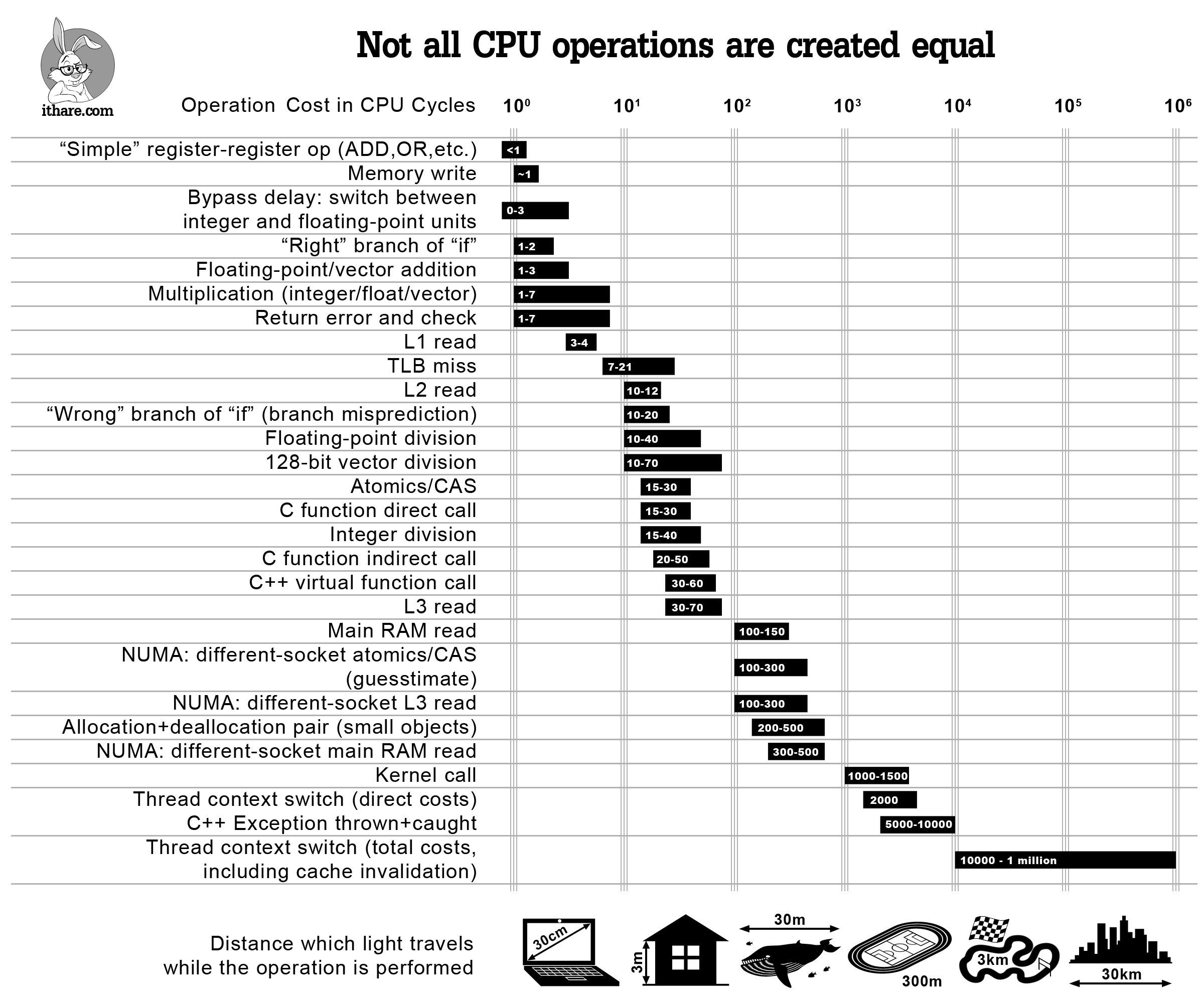

Упражнения

1) Посчитать количество примитивных операций в сортировке выбором.

public void SelectionSort(int[] a)                 // Количество операций
{ 
  for (int i = 0; i < a.Length; i++)               // n
  {                                                // n
      int minPos = i;
      for (int j = i + 1; j < a.Length; j++)       // n(n-1)/2
      {
        if (a[j] < a[minPos])                      // n(n-1)/2
          minPos = j;                              // n(n-1)/2
      }
    int temp = a[i];                               // n
    a[i] = a[minPos];                              // n
    a[minPos] = temp;                              // n
  }
}

Максимальное количество примитивных операций совершаемых алгоритмом равно $$5n + \dfrac{3 n(n-1)}{2} = \mathcal{O}(n^2)$$

2) Посчитать количество примитивных операций в алгоритме перемножения двух матриц.

public void MultiplyMatrix(int[,] a, int[,] b, int n)   // Количество операций
{ 
  int[,] c = new int[n, n];                             // 1

  for (int i = 0; i < a.Length; i++)                    // n
  {
    for (int j = 0; j < a.Length; j++)                  // n*n
    {
      int sum = 0;                                      // n*n
      for (int k = 0; k < a.Length; k++)                // n*n*n
        sum = sum + a[i, k] * a[k, j];                  // n*n*n
    }
    c[i, j] = sum;                                      // n*n
  }
}

Максимальное количество примитивных операций совершаемых алгоритмом равно $$1+n+3n^2+2n^3 = \mathcal{O}(n^3)$$.

МУСОР

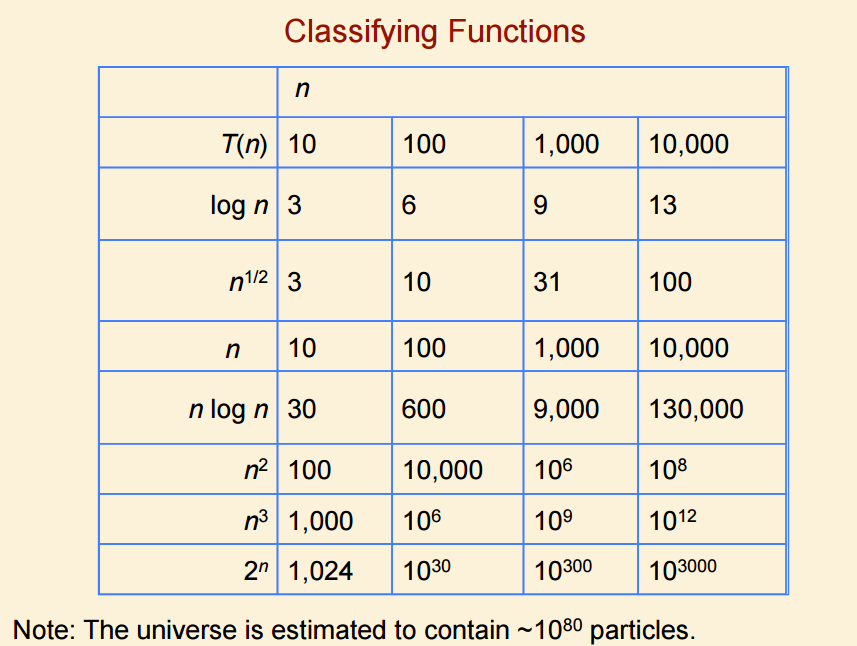
Seven functions that often appear in algorithm analysis:

– Constant ≈ 1

– Logarithmic ≈ log n

– Linear ≈ n

– N-Log-N ≈ n log n

– Quadratic ≈ n2

– Cubic ≈ n3

– Exponential ≈ 2n

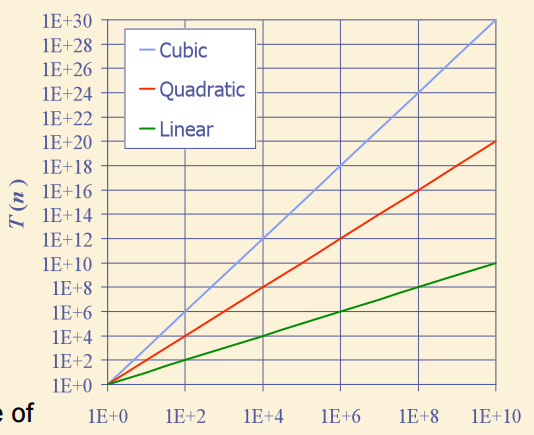
В log-log масштабе, наклон линии (угловой коэффициент) соответствует скорости роста функции.